As variáveis aditivas e não aditivas I: definições e propriedades

Ao realizar uma estimativa ou simulação de uma nova variável, é importante nos questionarmos sobre a propriedade aditiva desta, sua propriedade linear e conhecer sua definição. Se a variável não for aditiva, esse conhecimento permite avaliar metodologias e técnicas para estimá-la, realizando, por exemplo: simplificações, recorrendo à definição para estimar as variáveis que a definem ou aplicando domínios onde ela se comporte aproximadamente de forma linear.

Conhecer as variáveis permite estabelecer suas propriedades matemáticas, por exemplo, assumir sua linearidade ou propriedades geológicas para adotar critérios válidos que permitam conceptualizar seu comportamento (exemplo: estabelecer que a variável apresenta diferentes comportamentos de acordo com condições geoquímicas ou geofísicas); esse conhecimento nos permite, finalmente, extrapolar os valores no espaço e/ou tempo.

Mas como se define uma variável aditiva? Como se distingue uma variável aditiva de uma não aditiva? Quais são suas características? Como abordamos a estimativa de variáveis não aditivas?

Comecemos com a definição e propriedades das variáveis para compreender e diferenciar as variáveis aditivas das não aditivas:

Primeiro, uma variável aditiva é aquela que, na união de suas partes, corresponde à soma destas, por exemplo: comprimento (m), área (m²), volume (m³), tonelagem (massa). Por exemplo: 2(m³) + 3(m³) = 5(m³).

Segundo, vejamos os conceitos de propriedades extensivas e intensivas das variáveis. Uma propriedade é extensiva quando depende do tamanho, quantidade ou extensão do sistema. Essas variáveis são aditivas, como massa e volume; se combinarmos duas amostras, as propriedades extensivas se somam. Por exemplo, se tivermos dois objetos com massas de 2 kg e 3 kg, a massa total será 5 kg. Por outro lado, uma propriedade é intensiva quando não depende do tamanho, quantidade ou extensão do sistema. As propriedades intensivas, como densidade, temperatura e pressão, não se somam quando se combinam diferentes sistemas. Por exemplo, se temos um litro de água com densidade de 1 g/cm³ e adicionamos outro litro de água com a mesma densidade, a densidade total do sistema continua sendo 1 g/cm³ (não 2 g/cm³). Com esse exemplo da densidade, podemos estabelecer que ela não é uma variável aditiva sensu stricto, pois sua soma não resulta em 2 g/cm³.

Para incorporar essas variáveis intensivas, como densidade, às aditivas, devemos ampliar a definição de aditividade, incorporando a definição de funções lineares.

Terceiro, estabeleceremos um domínio (x,y) e incorporaremos a seguinte função y = 3x + 2 em um gráfico de coordenadas (x,y); como já sabemos, essa função corresponde a uma linha reta. Em seguida, podemos generalizar: y = a1x1 + a2x2 + … + anxn, onde a1 + a2 + … + an = 1, são os pesos atribuídos a cada amostra a1…an e devem ser definidos com base no denominador da definição da variável. No caso da densidade (ρ = m/V), utilizaremos o volume para determinar o peso “a” de sua fusão linear.

Agora, devemos detalhar a atribuição dos pesos (a1…an). Como exemplo, usaremos a definição de densidade ρ = m/V (g/cm³); a ponderação é realizada pelo denominador, neste caso, o volume, pois o denominador define o espaço matemático no qual a variável está definida. No exemplo a seguir, usaremos três amostras com volumes variados e massas distintas. Em seguida, misturamos essas amostras e calculamos sua densidade em laboratório (isso é importante porque, em variáveis não aditivas, o cálculo da mistura não se expressa materialmente; ao misturar duas amostras com valores diferentes, o valor obtido a partir do cálculo não condiz com o valor obtido em laboratório — mais adiante revisaremos esse efeito com a variável Work Index). Para isso, somamos o total das massas das amostras e o total do volume (medição de laboratório); o valor é encontrado em (a) da Tabela 1, que corresponde à densidade real.

Para obter a densidade total, aplicamos: Densidade = a1D1 + a2D2 + a3*D3, onde ai corresponde aos pesos calculados pelos seguintes métodos:

• Média aritmética (b), onde os pesos são calculados como ai = 1/n, sendo n o número de amostras. Porém, o resultado em (b) é diferente do obtido em (a), portanto, este método não é aplicável.
• Somar as densidades das amostras com os pesos obtidos ponderando as massas das amostras, ai = Mi/MT, onde Mi são as massas das amostras e MT a massa total. Porém, o resultado (c) não coincide com o valor de (a), portanto, este método não é aplicável.
• Somar as densidades das amostras com os pesos obtidos ponderando os volumes das amostras, ai = Vi/VT, onde Vi são os volumes das amostras e VT é o volume total. Neste caso, (d) = (a).

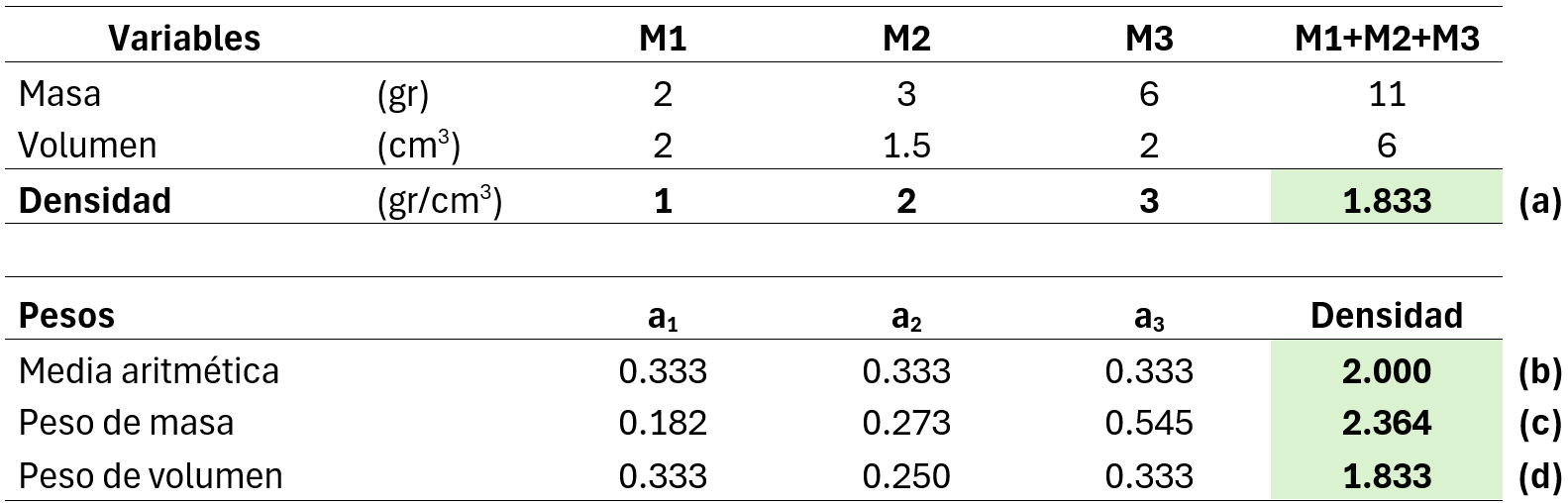
Isso indica que a unidade em que se mede o valor da variável encontra-se no denominador; portanto, para calcular a média da variável, devemos considerar o denominador para obter o valor da variável na mistura.

Com isso, estamos prontos para generalizar a aditividade das variáveis: uma variável será aditiva se a soma de suas partes permitir obter o valor do total, tal que y=a₁x₁ + a₂x₂ +…+ a_nx_n, onde se cumprem as seguintes restrições: se tivermos uma variável extensiva, a₁ = a₂ = a_n=1; se for uma variável intensiva, a₁ + a₂ +...+ a_n   =1.

Outras prop

Já mencionamos que a propriedade da linearidade nos permite calcular a mistura total a partir das amostras individuais, e também nos permite determinar a aditividade ou não de uma variável, calculando a mistura e comparando com a observação em laboratório. Funções lineares apresentam o princípio da superposição, que estabelece que a resposta total da amostra é a soma das respostas individuais de cada subamostra (lembrando que não estamos estimando, estamos calculando uma mistura de diferentes amostras).

Essa linearidade também é aplicável a variáveis cujo valor é gerado a partir de uma função baseada em outras variáveis. Para que uma variável gerada a partir de uma função seja aditiva, a função deve ser linear (até agora assumimos que as variáveis de origem são aditivas). Se uma variável não pode ser obtida por soma ou média ponderada direta, então estamos diante de uma variável não aditiva. Alguns exemplos de variáveis não aditivas são aquelas geradas com funções de dependência logarítmica, exponencial, etc.

Variáveis não aditivas são aquelas cujo valor médio não pode ser obtido por soma ou média ponderada direta, pois apresentam comportamento não aditivo (não linear). Um exemplo são variáveis como resistência e permeabilidade, em que a média não representa fielmente a realidade física.

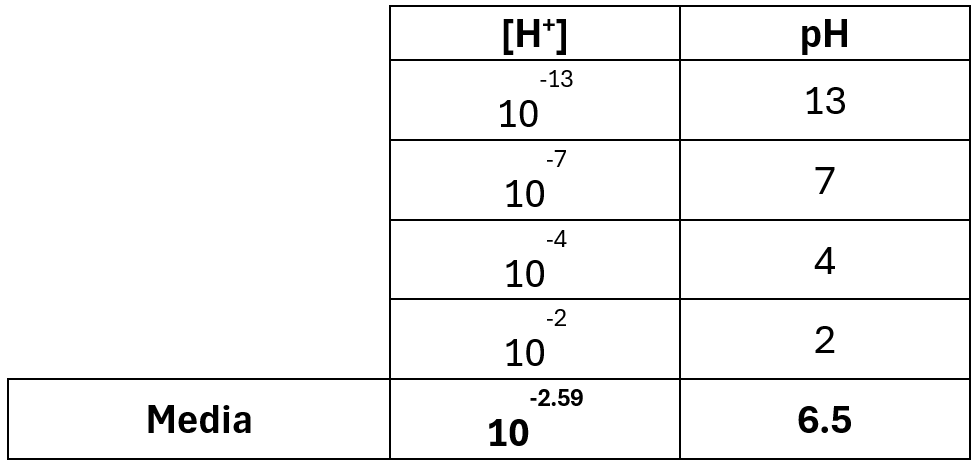
Vejamos este conceito com o exemplo da variável pH. Na Tabela 2, encontra-se a variável pH, definida como pH = -Log10[H+]; se obtivermos a média diretamente da definição de pH, o resultado é 6,5, entretanto, se obtivermos a partir da concentração, o pH é 2,59. Este exemplo mostra que não se pode obter médias a partir de funções não lineares, sendo necessário recorrer às definições para obter os resultados corretos. Em particular, aqui a média ponderada é obtida diretamente da concentração, transformando depois a concentração em pH.

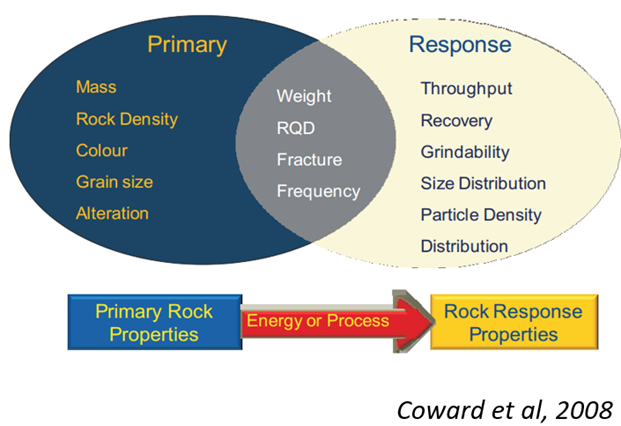
Existem outras propriedades de variáveis em áreas como geotecnia ou metalurgia que podem ser classificadas como primárias ou de resposta. Considera-se propriedade primária se representa uma característica intrínseca do material estudado, e propriedade de resposta se representa a característica de resposta do material a algum processo. Entre essas classificações, encontram-se propriedades intermediárias (ver Figura 1).

Variáveis de resposta são aquelas que correspondem ao resultado medido dentro de um ensaio, que pode ser influenciado por fatores que não estão na definição da variável. Em geral, variáveis de resposta são consideradas complexas e não lineares.

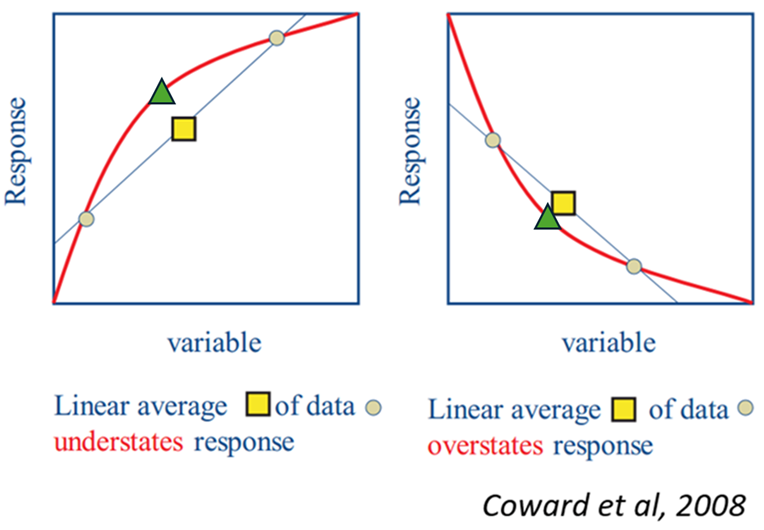
Na Figura 2, mostra-se o efeito de calcular a variável de resposta (quadrado) a partir de duas amostras (círculos); como não é linear, o resultado da mistura das duas amostras não condiz com a resposta delas (triângulo). Mais adiante, revisaremos esse problema com a variável Work Index.

Linearidade nas funções de estimação

Uma área relacionada à aditividade das variáveis é a geoestatística, ramo da estatística que analisa e modela a variabilidade espacial de fenômenos, focando na dependência espacial dos dados, ou seja, como a localização de uma medição afeta outras em seu entorno. Diferentemente da estatística clássica, que considera dados independentes do espaço, a geoestatística estuda fenômenos regionalizados (comportamento das variáveis em um volume determinado).

Grande parte dos métodos geoestatísticos envolve médias aritméticas ponderadas e dependentes do espaço, diferentemente da aditividade revisada anteriormente, que se relaciona à mistura de amostras e ao valor que toma com base nas amostras iniciais e no espaço matemático definido pela variável.

A seguir, revisaremos a equação de kriging e de simulação para entender a relação com variáveis aditivas.

O caso geral da função de estimação é:

Z(r)=b₁*Z(r₁) + b₂* Z(r₂) +...+ b_n* Z(r_n) 

O importante na estimação é que os pesos (b1…bn) estão relacionados tanto aos valores das variáveis quanto às suas relações espaciais, estabelecidas pelo comportamento variográfico.

No caso do kriging ordinário, a equação é definida da seguinte forma:

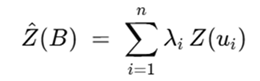
E no caso da equação geral de simulação condicional:

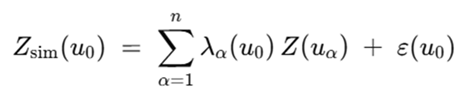
Ambas funções são lineares, portanto requer-se que as variáveis de entrada sejam aditivas e, consequentemente, lineares. Daí a importância da aditividade e linearidade das variáveis a estimar. A linearidade exigida na estimação é definida em um espaço tridimensional. Para o exemplo revisado da densidade, a aditividade também está definida no espaço (volume), e a estimação desta variável, que também requer linearidade no espaço, cumpre completamente os requisitos para sua estimação.

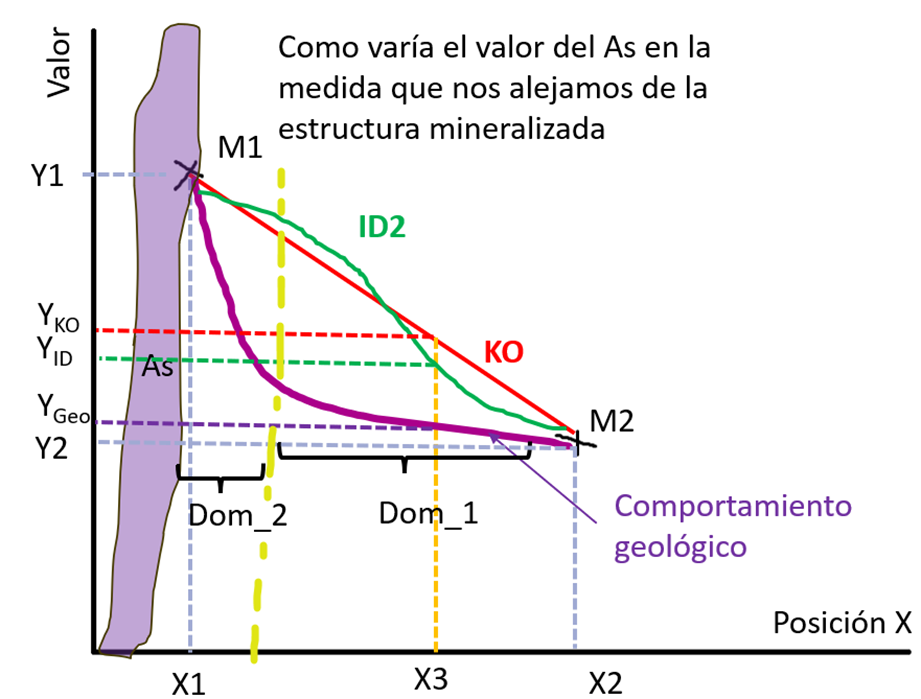
Agora, vamos revisar o comportamento espacial de uma variável localizada em diferentes domínios. No exemplo a seguir, mostra-se o comportamento do arsênico (As) ao nos afastarmos de um veio mineralizado de enargita (Cu₃AsS₄). Temos duas amostras (M1 e M2) com As e queremos determinar a lei (Y) em X3 (Figura 3). Na linha vermelha está a estimativa de kriging ordinário (KO), que é uma função linear; em verde, a estimativa do inverso da distância ao quadrado (ID2), que é uma função não linear; e a linha roxa representa o comportamento real do arsênico.

Com base neste exemplo, podemos estabelecer que, para usar modelos lineares de interpolação (em variáveis de comportamento não linear), é necessário separar, neste caso, pelo menos dois domínios entre X1 e X2, para que a variável se comporte aproximadamente de forma linear em seus respectivos domínios. Isso ocorre porque o comportamento da variável não é linear nessas condições (contato de dique mineralizado com rocha encaixante). Este exemplo demonstra a linearidade da função KO, a não linearidade da função ID2 e, por outro lado, a não linearidade do comportamento de uma variável; porém, ao restringir os domínios, podemos assumir um comportamento aproximadamente linear para aplicar métodos de estimação.

No próximo blog, será apresentado um exemplo de variável geotécnica e outro de variável metalúrgica para entender este tipo de variáveis não aditivas, suas definições, comportamento e como abordar a estimação com as restrições próprias dessas variáveis.