As variáveis aditivas e não aditivas III: revisando propriedades de aditividade e linearidade das concentrações do tipo %
Esta é a última entrada relacionada às variáveis aditivas e não aditivas. Lembrem-se de que vocês podem encontrar informações sobre variáveis não aditivas geotécnicas e metalúrgicas na nossa publicação anterior.
As concentrações de Cu (%) são aditivas e lineares?
A seguir, revisaremos as variáveis de concentração do tipo % em massa, definidas por:
Concentração (X) % = 100 * (massa)X / (massa)Tot, ou seja, a quantidade em gramas do elemento de interesse (X) em relação à massa total da amostra ((massa)Tot), multiplicada por 100 para obter a concentração em %. A Tabela 1 apresenta duas amostras utilizadas para determinar sua aditividade. Elas são separadas em três componentes para, posteriormente, entender o efeito da densidade. A amostra M_01 pesa 100 gramas (ver linha b), com 1 grama de Cu (ver linha a), 15 gramas de Mag e 84 gramas de ganga, resultando em 1% de Cu (ver linha c). Para a amostra M_02 obtém-se 2% de Cu. Na última coluna, ambas as amostras são misturadas e, aplicando-se a definição, obtém-se uma lei de 1,67% de Cu.

Para demonstrar sua aditividade, devemos obter o mesmo teor da mistura das amostras M_01 e M_02 usando a definição y=a1x1 + a2x2 +…+ anxn. Os pesos a1…an são dados pelo denominador da definição de concentração, que é a massa total. Assim, a concentração de Cu de M_01 + M_02 é:
Cu% M_01 + M_02 =(100gM_01/300gM_01_M_02) *1%CuM_01+(200 gM_02/300 g M_01_M_02) *2%Cu M_02=1.67
O valor obtido é o mesmo obtido aplicando-se a definição de teor em % e apresentado na Tabela 1 com a soma das amostras M_01 e M_02. Portanto, estamos diante de uma variável aditiva; em particular, ela é aditiva no espaço da massa total definido na concentração (X) %.
Agora, quando utilizamos essa variável para realizar estimativas espaciais, estas são feitas no espaço euclidiano 3D (volumétrico), e é nesse espaço — euclidiano ou volumétrico — que se assume um comportamento linear dos dados para as equações de KO ou simulações.
Como primeiro passo, vamos revisar a concentração de X (Cu, por exemplo) no espaço da massa total e no espaço volumétrico para entender como esses valores se relacionam ou se comportam.
Para simplificar o teor expresso entre 0 e 100%, o expressaremos entre 0 e 1.
Concentração de (X) no espaço da massa total:
(X) = (masa)Cu/(masa)Tot
Concentração de (X) no espaço euclidiano:
(X) = (masa)Cu/ (volumen)Tot = (masa)Cu/ (masa/ρ)Tot,
onde (masa)Cu = metal de interesse, (masa)Tot = massa total da amostra, (volumen)Tot = volume total e (masa/ρ)Tot = massa total da amostra dividida pela densidade da amostra.
Com essas relações podemos transformar as concentrações definidas no espaço da massa total em concentrações no espaço euclidiano.
Para este exercício, somente o denominador da definição (a massa total da amostra, (masa)Tot) é substituído a partir da definição de densidade, porque as densidades das diferentes amostras variam e dependerão da composição dos minerais presentes. Por outro lado, o numerador não é substituído pela definição de densidade, pois a densidade é a mesma em todas as amostras para o metal analisado, já que se trata do mesmo elemento e, portanto, possui densidade constante.
Para começar, transformaremos o teor de Cu de três amostras (M_01, M_02 e M_03) para visualização. Na Tabela 2 mostra-se que cada amostra contém Cu, magnetita e ganga, juntamente com suas respectivas densidades (d) e massas (a). As concentrações são expressas como a razão entre as massas (c) dentro do espaço de massa total. A partir das densidades de cada componente (e), convertemos as massas em volumes para obter o volume total (f), aplicando assim a definição de concentração volumétrica no espaço euclidiano.
Se compararmos a concentração volumétrica das amostras M_02 e M_03 com a da amostra M_01, a primeira coisa que se observa é que os volumes diferem entre elas, assim como suas concentrações volumétricas (h). Assim, enquanto no espaço da massa total as concentrações são iguais para todas as amostras, no espaço volumétrico essas mesmas amostras exibem concentrações distintas devido ao efeito das diferentes densidades.
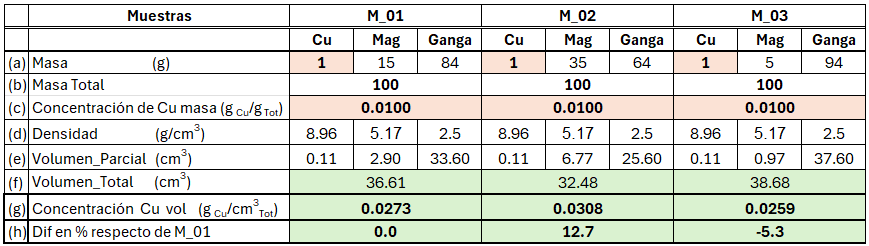
Desse exercício conclui-se que, ao estimar concentrações, a suposição de comportamento linear impacta de maneira distinta dependendo do espaço em que a variável de estimativa é definida. Quando a linearidade é aplicada à variável definida no espaço da massa total, exige-se implicitamente que tanto a quantidade de Cu quanto a densidade da amostra variem linearmente em conjunto — algo difícil de justificar conceitualmente. Em contrapartida, ao assumir linearidade para a variável de concentração definida no espaço volumétrico, o que se exige é que o conteúdo de Cu se comporte linearmente no espaço; isso é razoável, dado que tanto o espaço de estimativa quanto a variável estão definidos em um espaço volumétrico (euclidiano).
No caso da variável definida no espaço da massa total, o conteúdo de Cu só é conhecido após a estimativa da densidade, o que implica que a quantidade final de Cu depende diretamente dessa estimativa. Isso é relevante, porque nem sempre se dedica atenção suficiente à estimativa da densidade, apesar de seu impacto no resultado.
Para visualizar graficamente a relação entre as variáveis de concentração definidas no espaço da massa total e no espaço volumétrico, foi elaborada a Tabela 3 a partir das definições anteriores. Essa tabela contém 100 amostras cuja massa total é sempre de 100 g. Cada amostra é composta por Cu, magnetita (Mag) e ganga. O conteúdo de Cu é constante em todas as amostras (1 g), enquanto a quantidade de magnetita aumenta progressivamente de 0 g a 99 g, reduzindo-se na mesma proporção a ganga.
Para cada amostra calcula-se a concentração de Cu tanto no espaço da massa total (massa Cu / massa total) quanto no espaço volumétrico (massa Cu / volume total).
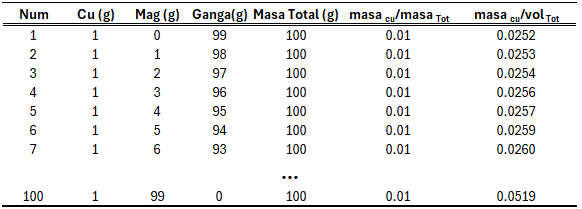
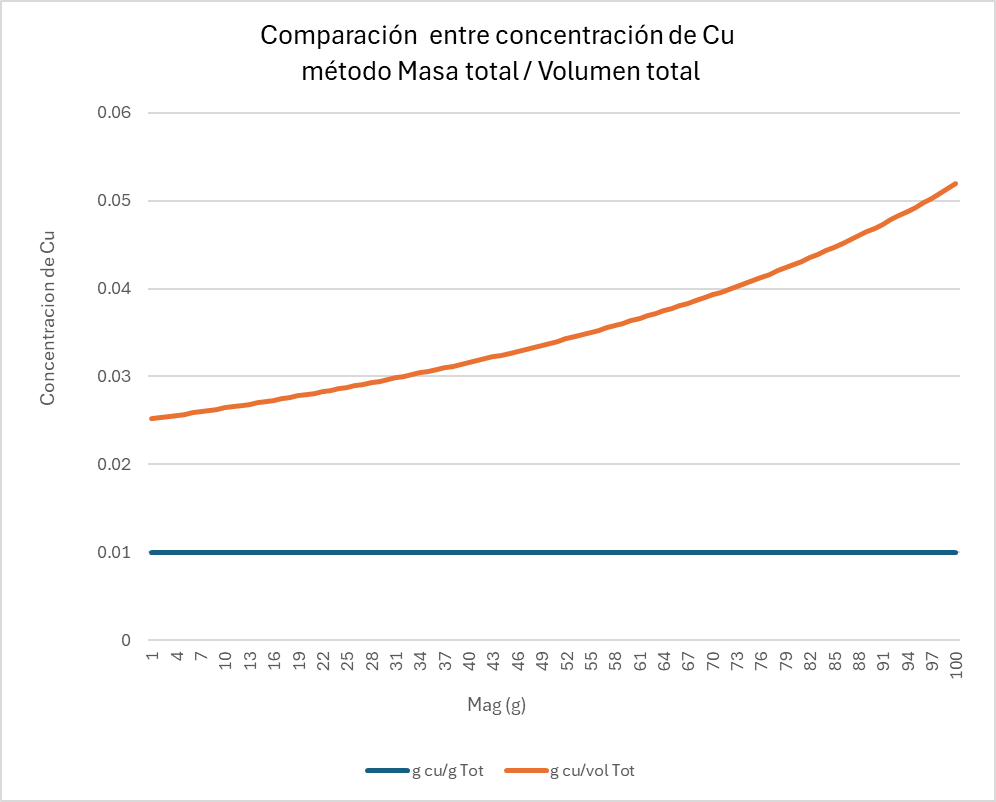
A partir dessa tabela, gera-se o gráfico apresentado na Figura 1. Observa-se que as definições das variáveis em ambos os espaços não apresentam comportamento linear. Enquanto a variável definida no espaço da massa total permanece constante, a concentração definida no espaço volumétrico aumenta à medida que a densidade cresce (resultado do maior conteúdo de magnetita). Além disso, o gráfico evidencia que a relação entre ambas as variáveis também não é linear.
No gráfico seguinte (Figura 2), gerado a partir de uma tabela semelhante à anterior, mas composta somente por Cu e ganga, o conteúdo de Cu é aumentado progressivamente e duas variáveis são representadas: a concentração de Cu definida no espaço volumétrico e a definida no espaço da massa total. O resultado mostra que a relação entre ambas é não linear.
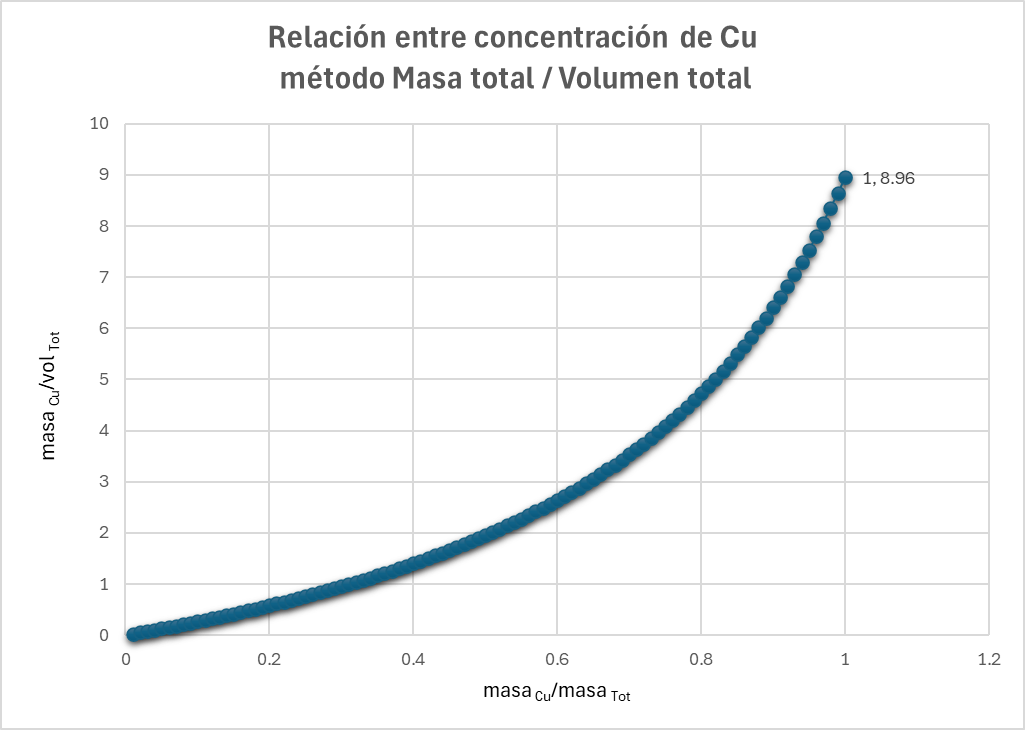
Como resumo, ambas as variáveis são aditivas em seus respectivos espaços (espaço da massa total e espaço volumétrico). Para ambas, devemos assumir linearidade ao estimar (seja por krigagem ou simulações). No entanto, no caso da concentração definida no espaço da massa total, a concentração de Cu se relaciona de forma não linear com o espaço euclidiano (volumétrico) da estimativa devido às variações de densidade entre as amostras. A relação entre ambos os tipos de concentração é expressa como: concentração CuV = concentração CuM × (massaTot / volTot).
Isso levanta a pergunta: como controlar esse comportamento não linear do dado no espaço euclidiano? Se a densidade fosse constante nas amostras, a não linearidade desapareceria. Por isso, uma estratégia consiste em definir domínios adequados que reduzam a variabilidade da densidade. Da mesma forma, amostras com densidades muito distintas podem ser tratadas como outliers. Além disso, como corolário, estabelece-se a importância crítica de estimar corretamente a densidade, já que ela determina a quantidade de Cu presente no depósito.
Por fim, embora a variável de concentração volumétrica seja plenamente compatível com o espaço de estimativa e permita obter diretamente o conteúdo de Cu sem envolver a densidade, ela apresenta uma desvantagem prática: medir o volume total é muito difícil. Por essa razão, a variável que realmente se mede e se utiliza é a do espaço da massa total. Ainda assim, é altamente recomendável realizar exercícios comparativos entre ambas as definições de concentração, pois eles permitem compreender melhor as variáveis que utilizamos de forma habitual e, sobretudo, reconhecer suas limitações para aplicar corretamente as definições, procedimentos, cálculos e estimativas.
Com isso encerramos a série sobre variáveis aditivas e não aditivas. Esperamos que tenha sido de seu interesse e que tenha permitido aprofundar esses conceitos. Convidamos vocês a ficar atentos às nossas próximas publicações.



