As variáveis aditivas e não aditivas II: Exemplos de variáveis não aditivas geotécnicas e metalúrgicas

Seguindo nossa série de publicações sobre variáveis aditivas e não aditivas, hoje falaremos sobre o caso das geotécnicas e metalúrgicas. Lembrem-se de que podem encontrar as definições básicas e propriedades em nossa publicação anterior.

Exemplo de variáveis geomecânicas

Nos exemplos a seguir, não se pretende abordar a estimativa das variáveis não aditivas, mas sim revisar elementos básicos que permitam estabelecer um modelo conceitual coerente e uma metodologia de estimativa que trate adequadamente o problema.

Antes da definição das variáveis geomecânicas, é necessário revisar os conceitos de rocha intacta, descontinuidade e maciço rochoso. As rochas são caracterizadas em função das propriedades do material que as compõe, tais como seu comportamento reológico (deformação dos materiais), sua densidade, sua porosidade, etc.

A rocha intacta corresponde exclusivamente ao material localizado entre descontinuidades, enquanto o maciço rochoso é o material que inclui as descontinuidades.

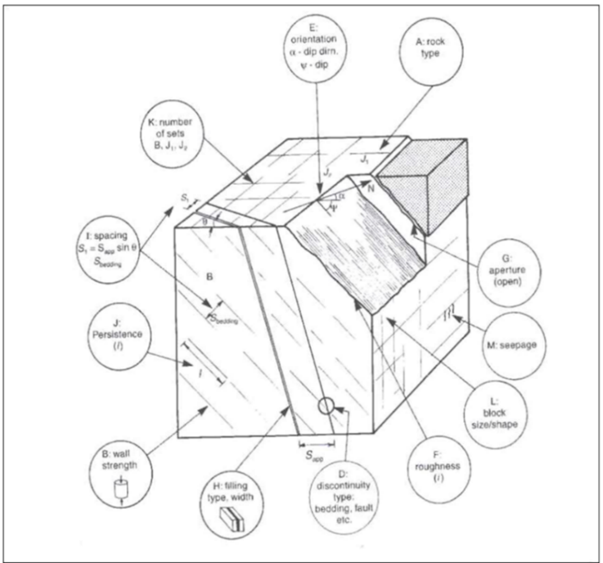
Para descrever uma zona, é necessário utilizar indicadores que considerem tanto as propriedades da rocha intacta quanto do maciço rochoso. A Figura 1 apresenta as variáveis de um maciço rochoso contidas na variável denominada Rock Mass Rating (RMR), desenvolvida por Z.T. Bieniawski entre os anos de 1972 e 1973 e atualizada posteriormente.

Variáveis não aditivas em geotecnia:

Entre as variáveis não aditivas em geotecnia estão a resistência ao cisalhamento (que depende da coesão e do ângulo de atrito), o módulo de deformação (não linear com tensões aplicadas) e o coeficiente de permeabilidade (relacionado de forma logarítmica com o tamanho dos poros). Essas variáveis requerem transformação ou modelagem especial, como uso de escalas logarítmicas, ou não são estimadas diretamente, mas sim a partir de seus componentes aditivos. Outros exemplos desse tipo de variáveis são: FF (Frequência de fratura), RQD (Rock Quality Designation), UCS (Uniaxial Compressive Strength), RMR (Rock Mass Rating), MRMR (Mining Rock Mass Rating), Q (Rock Tunneling Quality Index) e GSI (Geological Strength Index).

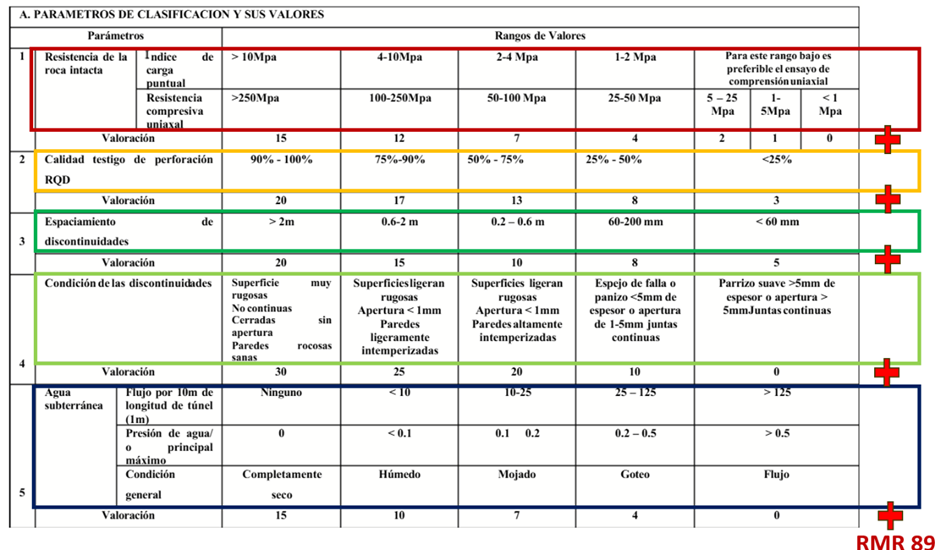
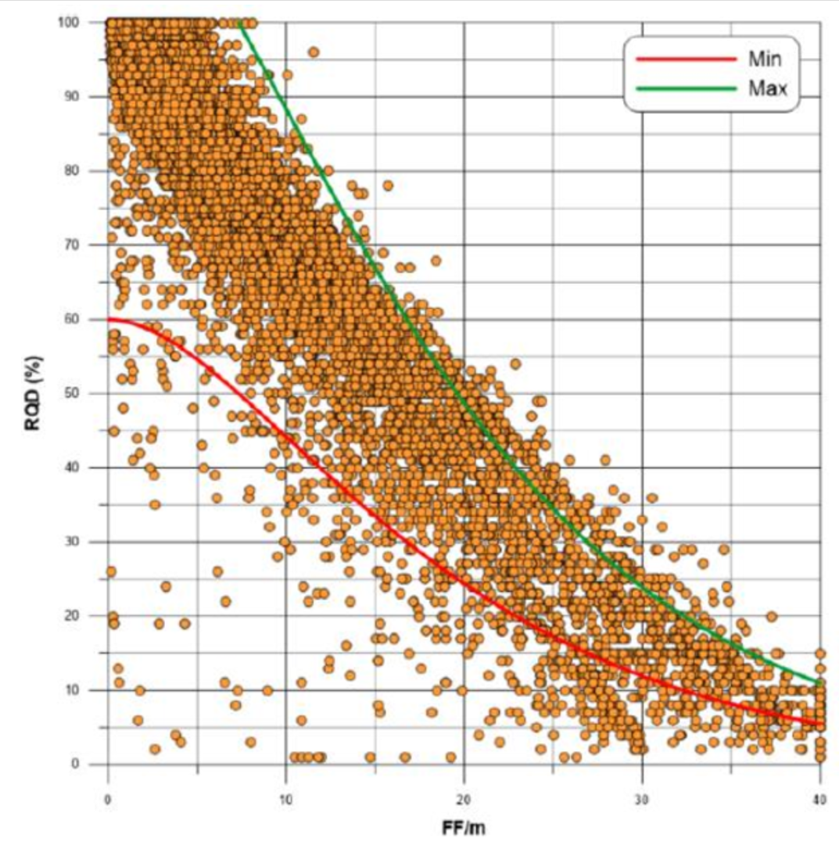
Na Tabela 3, é mostrada a composição da variável RMR, que corresponde à soma de variáveis parciais que permitem calcular a RMR; para isso, soma-se a pontuação de cada caixa colorida. Por exemplo, se o RQD da amostra é 65%, a pontuação atribuída é 13; esse cálculo é feito para cada uma das variáveis que compõem o RMR. Observando a pontuação atribuída a cada faixa da variável RQD, nota-se que não há relação linear com os valores medidos dessa variável, o que faz com que a RMR seja “não aditiva” e não linear, não podendo ser estimada diretamente. A recomendação é estimar cada variável separadamente e calcular posteriormente sua pontuação. Deve-se considerar que variáveis como RQD, FF e resistência da rocha intacta são variáveis direcionais, portanto não são aditivas, mas podem ser estimadas sob certas condições.

Variáveis direcionais:

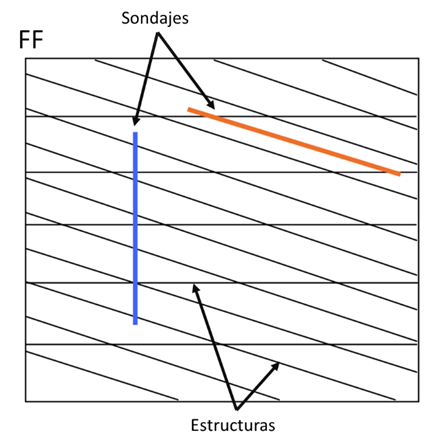
Quando falamos de variáveis direcionais, devemos entender que a orientação espacial na qual a variável é medida condicionará o valor da amostra, ou seja, depende da direção em que é medida, como FF, RQD e resistência à compressão.

Na Figura 2, as linhas vermelhas e azuis representam suportes de um metro de comprimento; é fácil verificar que, na direção vertical (azul), FF = 9 [fraturas/m]; enquanto para a sondagem inclinada (vermelha), FF = 2 [fraturas/m]. Esse simples exemplo mostra a grande dependência da direção que a variável pode ter.

O mesmo ocorre com outras variáveis geotécnicas como o RQD. No caso do RMR, depende, entre outras coisas, do espaçamento entre descontinuidades e do RQD, ambas variáveis direcionais. Para estimar essas variáveis, podemos estabelecer que o valor utilizado será o de menor qualidade, de modo que os valores estimados representem a pior condição, e que essa condição se reflita no valor do RMR; também ajuda estabelecer domínios com baixa variância dos dados. Devemos considerar que rochas com maior plasticidade, como tufos, ou que apresentem alto teor de argilas por alteração, apresentarão menor quantidade de estruturas que rochas submetidas ao mesmo esforço, mas mais rígidas, como basaltos não alterados. Em resumo, estabelecer domínios geológicos ajuda a enfrentar a estimativa de variáveis não aditivas.

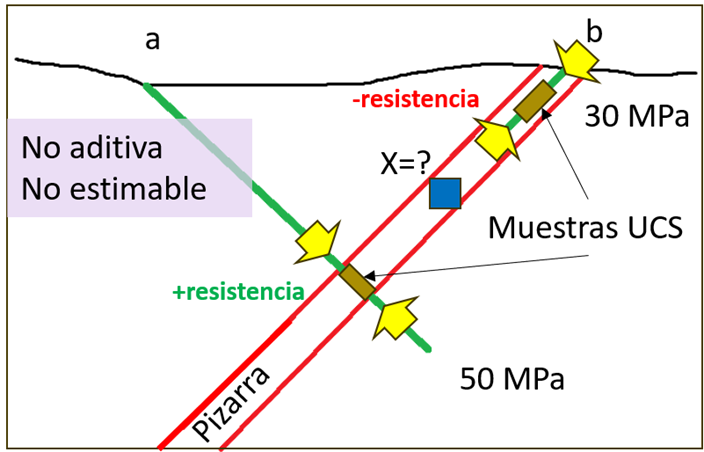
Outro caso é a variável resistência da rocha intacta. Ao medir, por exemplo, a variável UCS (Uniaxial Compressive Strength) em uma rocha metamórfica (ardósia), como mostra a Figura 6, pelo fato de serem medidas em diferentes direções, seus valores serão diferentes, pois as medidas realizadas paralelas ao eixo máximo de deformação são mais baixas que as realizadas perpendiculares a este. Essa variável apresenta variações direcionais relacionadas aos elipsoides de deformação nas rochas metamórficas, mas se as medidas forem realizadas em rochas intrusivas, podemos assumir um comportamento isotrópico, além de assumir aditividade nos diferentes domínios litológicos; portanto, podemos realizar estimativas dessas variáveis em cada domínio. O contexto geológico permite simplificar o problema desse tipo de variável.

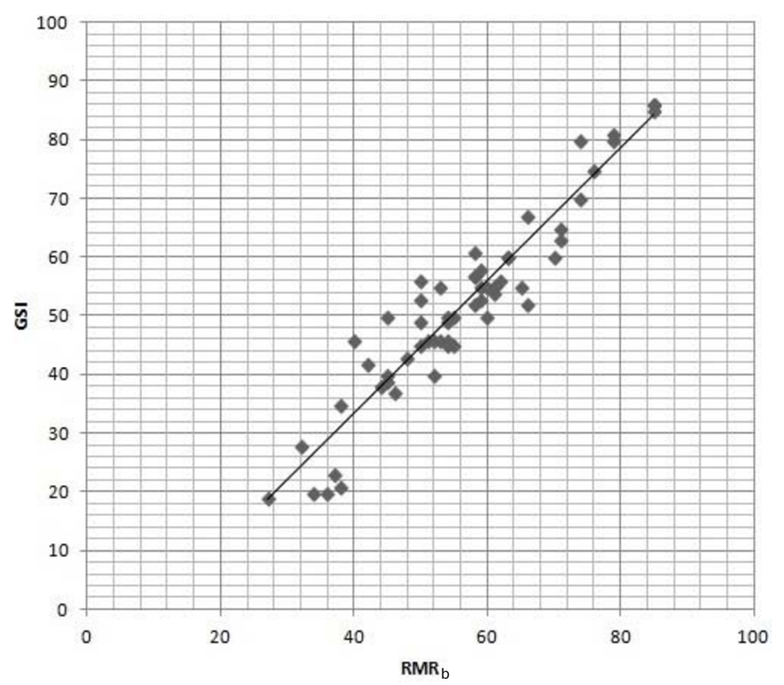
Outra propriedade importante das variáveis geotécnicas é a correlação existente entre elas. Por um lado, essas correlações apresentadas pelos dados também devem ser observadas no modelo estimado, podendo ser utilizadas como uma das validações das estimativas realizadas (ver Figura 4 e Figura 5). Por outro lado, essas mesmas relações entre as variáveis podem ser usadas na estimativa, por exemplo, pelo método dos resíduos, que permite conservar tanto a correlação entre variáveis quanto sua variabilidade.

Exemplo de variáveis metalúrgicas

Agora analisaremos a variável de resposta Work Index (Wi), definida como o índice de trabalho que requer a potência necessária para moer um material desde um tamanho teoricamente infinito até um tal que passe 80% dos 100 micrômetros, permitindo assim obter uma boa estimativa da energia necessária para a moagem (kWh/tc). Para calcular o índice Wi, devem ser obtidos dados experimentais sob rigorosas condições de operação.

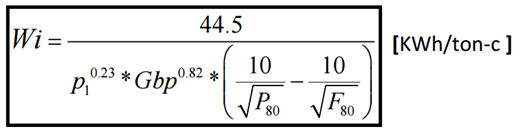
Cálculo para obter o Wi para moinho de bolas, onde:

• P80 [µm] é o tamanho da peneira que deixa passar 80% do produto final.
• F80 [µm] é o tamanho da peneira que deixa passar 80% do material de alimentação.
• Gbp [g/rev] refere-se aos gramas por revolução; corresponde ao índice de moabilidade (grindability) do moinho de bolas e é uma variável de resposta de um ensaio.
• p1 [µm] corresponde à abertura da malha de corte utilizada para fechar o circuito (tamanho 100% passante do produto).

Yan & Eaton (2003) estudaram o comportamento do índice de Bond em misturas físicas de minério de alta (Wi = 14,0 kWh/t) e baixa competência (Wi = 6,0 kWh/t). Consideraram que a mistura deveria corresponder à média aritmética dos valores inseridos (Wi = 10,0 kWh/t). No entanto, a mistura física testada em laboratório apresentou um valor de 12,23 kWh/t (Figura 6).

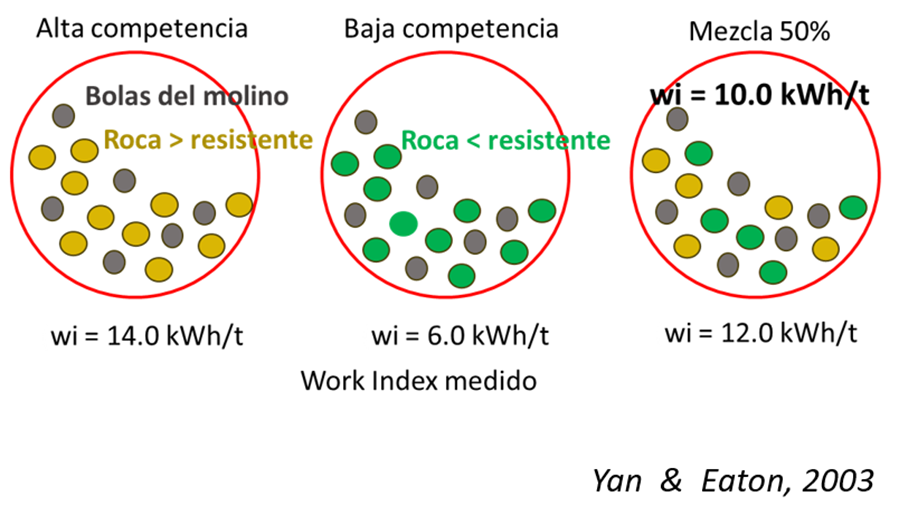
Essa diferença se deve à definição da variável: sendo uma função de resposta (ensaio) a um tratamento (kWh/t), não considera variáveis internas das amostras nem do sistema, portanto não responde a todas as condições de mistura, como a mencionada anteriormente, onde o material macio atua como amortecedor do material mais resistente, permanecendo mais tempo no moinho para atingir o tamanho desejado.

Uma forma de lidar com esse tipo de variável é agrupar os dados em domínios com baixa dispersão, evitando a mistura de materiais com competências muito diferentes. Como, de qualquer forma, o material será misturado na planta, é possível testar diferentes proporções de misturas e atribuir os valores a partir de uma regressão ou outro método aos blocos que apresentem faixas de mistura.

Esse exemplo mostra a necessidade de conhecer o comportamento das variáveis de resposta ao misturar amostras com características distintas (ensaios). Neste exemplo, a fórmula não indica o teor de argilas como variável (que poderia modificar o resultado), e é justamente esse mineral que, em certas condições, gera uma resposta inesperada do ensaio. Por isso, é importante conhecer o ensaio e o depósito para revisar quais condições são modificáveis e testá-las.

No próximo blog, apresentar-se-á a variável concentração de Cu em %. Revisar-se-ão suas propriedades e características, de modo que possamos entender este tipo de variáveis e que considerações devemos considerar na hora de estimar.