blog informativo

Mais allá do kriging: o papel das simulações condicionais na avaliação de recursos

Nos últimos anos, as simulações condicionais ganharam um lugar cada vez mais importante na avaliação de Recursos Minerais. Hoje são cada vez mais exigidas em projetos e em minas em operação, devido aos seus múltiplos usos. No entanto, por sua alta complexidade, elas ainda não são utilizadas de forma transversal na indústria.

No blog a seguir, aprenderemos o que são, o que as diferencia dos estimadores lineares tradicionais e alguns de seus usos em casos reais trabalhados na GeoEstima.

O que são as simulações geoestatísticas?

São uma aplicação da simulação de Monte Carlo a variáveis regionalizadas que permitem quantificar a incerteza dos modelos. As técnicas de simulação geoestatística geram um grupo de realizações ou realidades com igual probabilidade de ocorrência. Se existe maior variabilidade nos dados ou existem menos dados para gerar o modelo, as realizações terão um maior grau de diferença entre si (Abzalov, 2016).

Dependendo de sua aplicação, podem ser usadas em variáveis categóricas (litologias, zonas minerais, alterações) ou em variáveis contínuas (teores, densidade, recuperações) (Rossi & Deutsch, 2014; Chiles & Delfiner, 2012). Normalmente, utilizamos simulações condicionais, que restituiem os valores medidos nos locais com dados. Portanto, esses locais com informação não terão incerteza.

Os modelos gerados têm a particularidade de reproduzir a distribuição ou histograma dos dados (proporção de valores altos, baixos, médios e variância) e o variograma (continuidade espacial, anisotropias e efeito pepita) (Rossi & Deutsch, 2014). A ideia das simulações condicionais é construir uma representação do fenômeno que seja consistente com os dados e que reproduza as flutuações locais: não é a realidade, mas uma possível versão dela (Chiles & Delfiner, 2012).

Entre algumas considerações práticas que devem ser levadas em conta, está a necessidade de calcular os pesos de desagrupamento das amostras para poder ter uma distribuição representativa do fenômeno e não uma distribuição enviesada pelo amostragem preferencial. Outro fator importante é a definição de domínios, já que as simulações condicionais são sensíveis à não estacionaridade. Para utilizar simulações, é necessário transformar os dados para o espaço gaussiano previamente (média zero, variância um), o que é feito por meio de uma função chamada anamorfose. Finalmente, as simulações representam os teores ou valores em suporte pontual e seus resultados devem ser rebloqueados (reagrupados) para o suporte de interesse (SMU).

Existem diversos algoritmos de simulação geoestatística disponíveis em muitos softwares comerciais. Algumas técnicas para simular variáveis contínuas são o algoritmo sequencial gaussiano (SGS) e o algoritmo de bandas rotativas (TB). Da mesma forma, entre os algoritmos populares para simular variáveis categóricas estão a simulação sequencial de indicadores (SIS), a simulação multiponto (MPS) ou a simulação plurigaussiana hierárquica truncada (HTPG).

Estimativa vs simulação

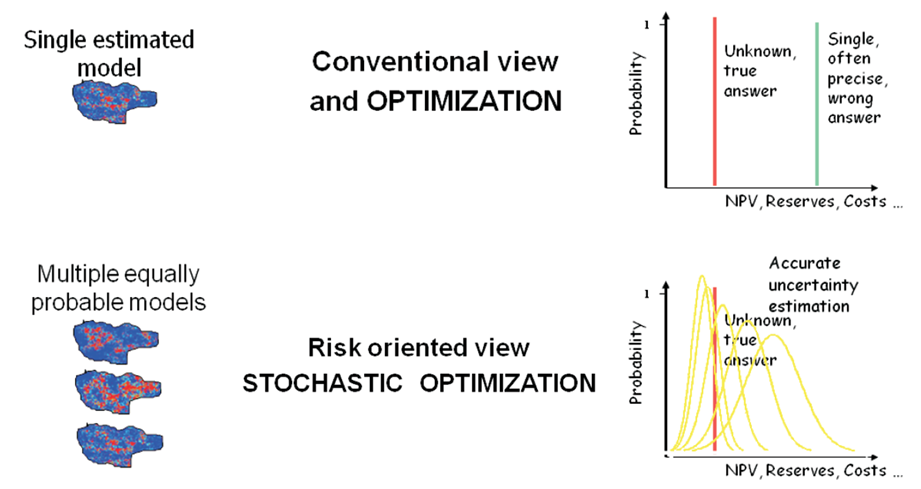
As estimativas fornecem um valor que, em média, se aproxima da realidade desconhecida. É uma combinação linear dos dados disponíveis, não tendenciosa, tem o menor erro quadrático e inevitavelmente apresenta suavização (mínimos maiores e máximos menores que os dados). As estimativas fornecem o valor esperado.

As simulações, por outro lado, são modelos não lineares, reproduzem a variabilidade dos dados, o que implica que preservam os valores extremos (não suavizam). As simulações produzem um conjunto de valores para cada ponto, permitindo quantificar a incerteza. Elas reproduzem corretamente a proporção de valores altos e baixos.

Tabela 1: Resumo comparativo estimativas e simulações

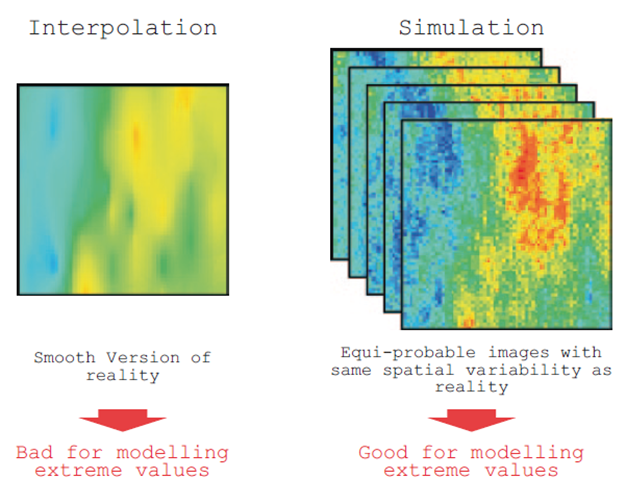
Na Figura 1 observa-se como o modelo estimado, ao ser suavizado, mostra valores mínimos mais altos e valores máximos mais baixos, enquanto que as simulações, por serem não suavizadas, reproduzem melhor os valores baixos e altos. Além disso, observa-se como a estimativa é um único modelo, enquanto que as simulações são N modelos com igual probabilidade de ocorrência.

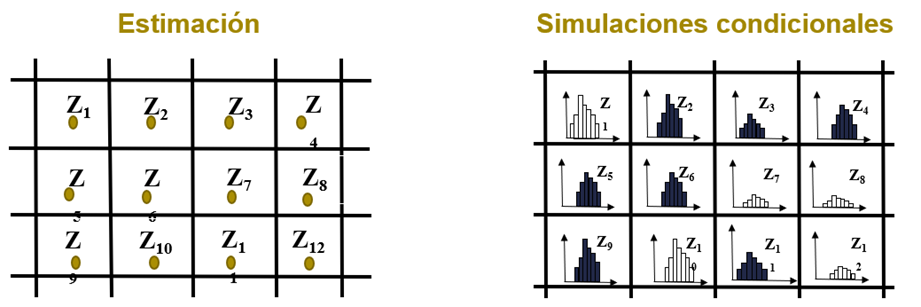
Figura 1: Estimativa vs simulação (Rossi & Deutsch, 2014)

Como mencionado, as estimativas entregam um único valor em cada bloco do modelo, enquanto que as simulações, ao serem N modelos, entregam uma distribuição de valores para cada bloco (Figura 2).

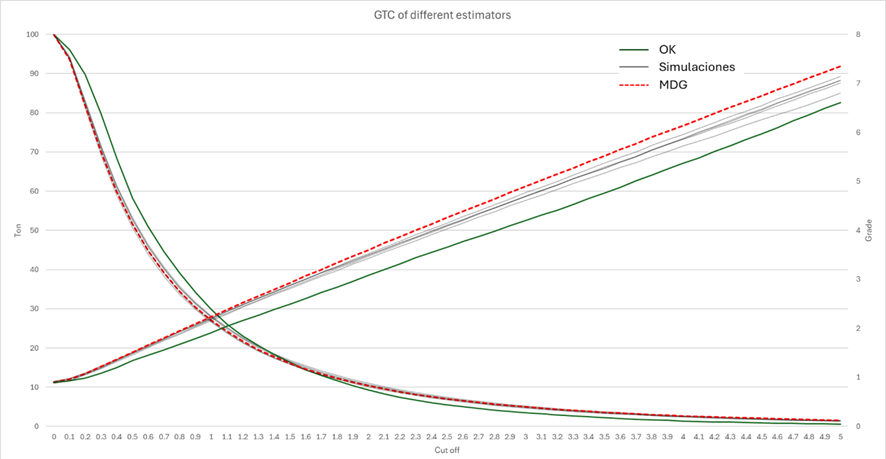
Figura 2: Estimativa vs simulação em cada bloco

Se utilizarmos o modelo de discreto gaussiano como referência, podemos observar a diferença entre um modelo estimado por kriging e um modelo simulado em termos de curva tonelagem-teor: o kriging, ao suavizar, reporta mais tonelagem de baixa lei e menos tonelagem de alta lei, enquanto que as simulações não têm essas divergências. Da mesma forma, o kriging sempre reporta uma menor lei média a corte maior que zero (sendo insesgado somente a lei de corte 0), em contraste com as simulações condicionais. Para essa comparação, as simulações pontuais foram promediadas ao suporte de SMU, igual ao do kriging.

Figura 3: Curva tonelagem-teor modelo tradicional vs simulações

Por que usar simulações?

Devido ao alto risco que qualquer projeto minerário representa, a incerteza — e o consequente risco — deve ser quantificada para uma melhor tomada de decisões.

A vantagem das simulações frente às estimativas tradicionais é que, a partir delas, podemos gerar modelos de incerteza a partir dos quais podem ser realizados diversos tipos de estudos: análise de riscos, quantificação da incerteza tanto de geologia quanto de teores, definição de categorias de recursos, estudo de potencial de mineralização e estudos de otimização do espaçamento de sondagens e, recentemente, planejamento estocástico.

Como integrá-las corretamente ao fluxo de trabalho?

Embora as simulações sejam normalmente utilizadas para quantificar a incerteza dos teores, limitar o estudo de simulações apenas a isso é um erro, porque a ideia é sempre integrar a maior quantidade de fontes de incerteza do modelo para não ter apenas uma visão parcial.

Quando possível, recomenda-se quantificar a variabilidade em cada etapa do estudo de recursos, seguindo um fluxo de trabalho hierárquico e uma configuração de uma-a-uma realização. A Figura 4 mostra de forma esquemática a integração da incerteza nas diferentes etapas do modelo, seguindo a configuração uma-a-uma e transferindo a incerteza em cada etapa (Deutsch, 2018; Deutsch, 2021).

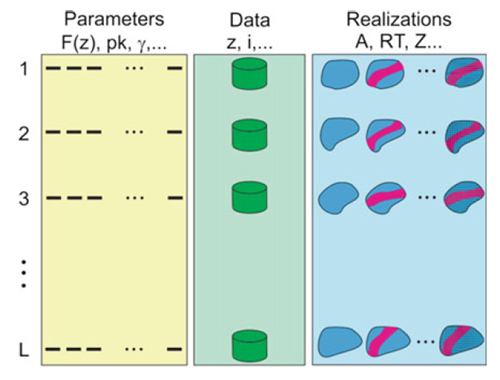
Figura 4: Simulações em cada etapa do fluxo de trabalho (Deutsch, 2021)

Incerteza dos dados: em caso de estudo multivariável, se existem bases de dados heterotópicas, recomenda-se imputar os dados faltantes gerando realizações destes e integrando essas realidades uma a uma ao estudo.
Incerteza de parâmetros: é possível realizar Bootstrap espacial para quantificar a incerteza no histograma dos dados.
Incerteza da geologia: a geologia apresenta uma variabilidade intrínseca que impactará diretamente os volumes mineralizados e o tonelagem reportado; portanto, quantificar a variabilidade dos contatos é crucial para compreender a variabilidade total do fenômeno que está sendo modelado.
Incerteza dos teores: é a etapa do fluxo que normalmente é realizada; consiste na quantificação da incerteza dos teores de interesse (minerais econômicos e contaminantes, quando aplicável). No caso de um estudo multivariável, deve-se decidir entre realizar co-simulações ou simular fatores independentes (transformações como PPMT – projection pursuit multivariate transformation ou MAF – Min-max autocorrelated factor), de modo que as simulações resultantes preservem as correlações dos dados e outras estruturas complexas decorrentes de heteroscedasticidade ou não linearidades.

Dessa forma, ao integrar a incerteza em cada etapa sucessiva, o resultado final será um reflexo muito mais fiel da variabilidade total do processo e a análise subsequente será muito mais robusta.

Exemplos de uso

A seguir são apresentados casos práticos de grandes operações onde as simulações entregaram bons resultados e levaram a uma melhor tomada de decisões.

Quantificação da incerteza geológica

A partir das simulações condicionais, foi calculada a variável entropía, que resume a incerteza do modelo geológico. A partir desta medida, é possível definir zonas em que o modelo é mais incerto e que, portanto, requer uma maior quantidade de informação (sondagens) para ser corretamente caracterizado (Figura 5). Isso pode ajudar no planejamento de novas perfurações (Figura 6) ou conduzir medidas de mitigação, como a mistura de materiais e ajustes no plano de mina para evitar frentes com alta entropia.

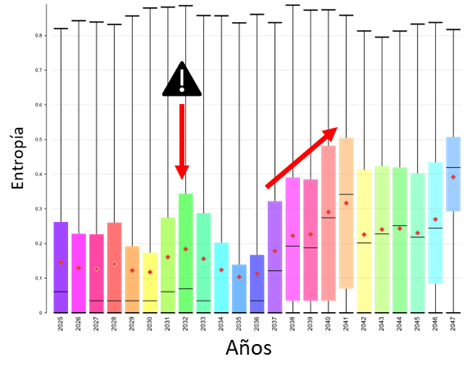
Figura 5: Zonas de alta entropia no plano de mina

Figura 6: Recomendação de novas sondagens (em preto) em zonas de alta incerteza geológica

Estudos de malha para a definição da categoria de recursos

Com base em um estudo de simulação, amostragem artificial e re-simulação, é possível quantificar a relação entre o espaçamento de sondagens e a incerteza — isto é, medir quanto a variabilidade do depósito diminuirá com a chegada de novas informações. Relacionando isso com um erro tolerado e um nível de confiança, podemos definir as malhas de sondagens necessárias para as categorias medido e indicado. A vantagem desse estudo sobre outras ferramentas de categorização é que a incerteza é medida diretamente e integra tanto a variabilidade da geologia quanto dos teores, além de permitir medir o erro em relação a uma lei de corte.

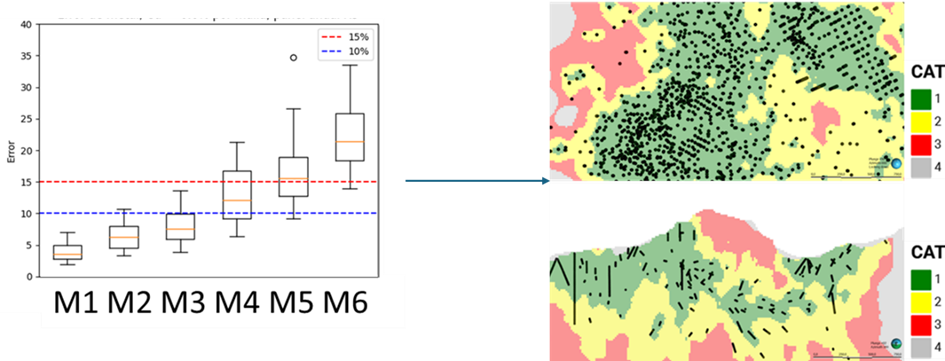
Figura 7: Incerteza vs espaçamento e categorização de recursos

Análise de risco de curto prazo

A partir do modelo simulado, gerou-se um indicador de confiança de 90 % de ser rocha mineralizada e de ultrapassar a lei de corte operacional. Esse indicador foi cruzado com o modelo de recursos oficial e identificou blocos que, no modelo determinístico, eram considerados rocha mineralizada e acima da lei de corte, mas que as simulações mostraram baixa probabilidade de realmente serem assim. Ao revisar esse indicador com reconciliations, observou-se correlação com resultados deficientes do modelo oficial. Dessa forma, o indicador foi utilizado pela equipe de curto prazo para identificar fases e bancadas com alta probabilidade de erro (blocos em vermelho na Figura 8).

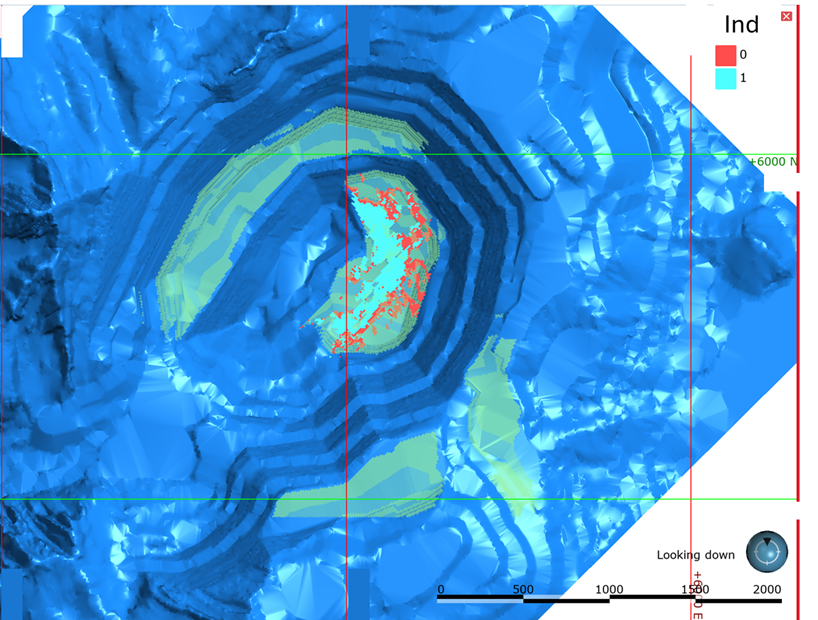
Figura 8: Indicador, em vermelho, zonas de alto risco (baixa probabilidade de serem conforme o planejado)

Planejamento estocástico

Os modelos simulados de geologia e teores podem ser utilizados como entrada para algoritmos de planejamento estocástico. Recentemente, a GeoEstima finalizou um modelo para um depósito de classe mundial de Cu em que foram simuladas zonas minerais, litologias e teores de Cu, CuS e Mo. Esses modelos serão utilizados para integrar a incerteza do depósito ao design da mina, ao plano de produção e na avaliação econômica de projetos e operações. Os fluxos estocásticos aumentam em até 15% o tonelagem total quando comparados ao planejamento tradicional. Além disso, foi demonstrado um aumento de até 10% no VAN entre o planejamento estocástico e o tradicional (Dimitrakopoulos, 2018).

Figura 9: Abordagem tradicional vs estocástica (modificado de Dimitrakopoulos, 2018)

As simulações condicionais estão revolucionando a forma como entendemos a incerteza na mineração. Você já trabalhou com elas? Quer saber como podem ajudá-lo a tomar melhores decisões e reduzir riscos em seus projetos?

Referências

Abzalov, M. (2016). Applied mining geology (Vol. 12).
Chiles, J.-P., & Delfiner, P. (2012). Geostatistics : Modeling Spatial Uncertainty. John Wiley & Sons.
Deutsch, C. V. (2018). All Realizations All the Time. In Handbook of Mathematical Geosciences (pp. 131–142). Springer International Publishing. https://doi.org/10.1007/978-3-319-78999-6_7
Deutsch, C. V. (2021). Implementation of Geostatistical Algorithms. Mathematical Geosciences, 53(2), 227–237. https://doi.org/10.1007/s11004-020-09884-z
Dimitrakopoulos, R. (2018). Stochastic Mine Planning—Methods, Examples and Value in an Uncertain World. In: Dimitrakopoulos, R. (eds) Advances in Applied Strategic Mine Planning
Emery, X. (2015). Geoestadística. Ingenierìa de Minas, Universidad de Chile.
Rossi, M. E., & Deutsch, C. V. (2014). Mineral Resource Estimation. In Mineral Resource Estimation. Springer Netherlands. https://doi.org/10.1007/978-1-4020-5717-5